Πώς να βρείτε την ακτίνα ενός κύκλου: για να βοηθήσετε τους μαθητές
Πώς να βρείτε την ακτίνα ενός κύκλου; Το ερώτημα αυτό είναι πάντα κατάλληλο για τους μαθητές που μελετούν την πλασματολογία. Παρακάτω θα εξετάσουμε διάφορα παραδείγματα σχετικά με τον τρόπο αντιμετώπισης του έργου.
Ανάλογα με την κατάσταση του προβλήματος, μπορείτε να βρείτε την ακτίνα του κύκλου όπως αυτή.
Τύπος 1: R = A / 2π, όπου A είναι το μήκος του κύκλου, και π είναι μια σταθερά ίση με 3.141 ...
Τύπος 2: R = √ (S / π), όπου S είναι η περιοχή του κύκλου.
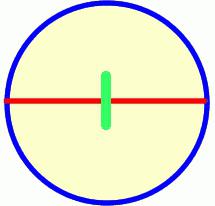
Φόρμουλα 3: R = D / 2 όπου D - είναι η διάμετρος του κύκλου, δηλαδή το μήκος του τμήματος που, που διέρχεται από το κέντρο του σχήματος συνδέει τα δύο μέγιστα σε απόσταση μεταξύ τους σημεία.
Πώς να βρείτε την ακτίνα του περιγεγραμμένου κύκλου
Πρώτον, ας ορίσουμε τον ίδιο τον όρο. Ονομάζεται κύκλος που περιγράφεται όταν αγγίζει όλες τις κορυφές ενός συγκεκριμένου πολυγώνου. Θα πρέπει να σημειωθεί ότι είναι δυνατόν να περιγράψουμε έναν κύκλο μόνο γύρω από ένα τέτοιο πολύγωνο, οι πλευρές και οι γωνίες του οποίου είναι ίσες μεταξύ τους, δηλαδή γύρω από ένα ισόπλευρο τρίγωνο, ένα τετράγωνο, ένα κανονικό ρόμβο και ούτω καθεξής. Για να λυθεί το πρόβλημα, είναι απαραίτητο να βρεθεί η περίμετρος του πολυγώνου, και επίσης να μετρηθούν οι πλευρές και η περιοχή του. Επομένως, οπλίστε τον εαυτό σας με ένα χάρακα, μια πυξίδα, μια αριθμομηχανή και ένα σημειωματάριο με ένα στυλό.
Πώς να βρείτε την ακτίνα ενός κύκλου, αν περιγράφεται γύρω από ένα τρίγωνο
Φόρμουλα 1: R = (A * B * Β) / 4S, όπου τα Α, Β, C, - το μήκος των πλευρών τριγώνου, και S - περιοχή του.
Τύπος 2: R = A / sin a, όπου A είναι το μήκος μιας πλευράς του σχήματος και η αμαρτία a είναι η υπολογιζόμενη τιμή του ημιτονοειδούς της γωνίας απέναντι από αυτή την πλευρά.
Η ακτίνα του κύκλου, η οποία περιγράφεται γύρω από ένα ορθό τρίγωνο.
Τύπος 1: R = B / 2, όπου Β είναι η υποτείνουσα.
Φόρμουλα 2: R = M * B, όπου B είναι η υποτείνουσα, και M είναι η διάμεσος που τραβιέται προς αυτήν.
Πώς να βρείτε την ακτίνα ενός κύκλου, αν περιγράφεται γύρω από ένα κανονικό πολύγωνο
Τύπος: R = A / (2 * sin (360 / (2 * n))), όπου A είναι το μήκος μιας πλευράς του σχήματος και n είναι ο αριθμός πλευρών σε δεδομένη γεωμετρική μορφή.
Πώς να βρείτε την ακτίνα ενός εγγεγραμμένου κύκλου
Ένας εγγεγραμμένος κύκλος ονομάζεται όταν αγγίζει όλες τις πλευρές ενός πολυγώνου. Ας εξετάσουμε μερικά παραδείγματα.
Τύπος 1: R = S / (P / 2), όπου - S και P - η περιοχή και η περίμετρος του σχήματος, αντίστοιχα.
Τύπος 2: R = (P / 2 - A) * tg (a / 2), όπου P - περίμετρος, Α - το μήκος μιας πλευράς, και - η γωνία αντίθετη προς αυτή την πλευρά.
Πώς να βρείτε την ακτίνα ενός κύκλου αν είναι εγγεγραμμένη σε ένα ορθογώνιο τρίγωνο
Τύπος 1:
Η ακτίνα του κύκλου, που είναι εγγεγραμμένη στο ρομβο
Ο κύκλος μπορεί να εγγραφεί σε οποιοδήποτε ρόμβο, τόσο ισόπλευρο όσο και μη ισόπλευρο.
Τύπος 1: R = 2 * H, όπου H είναι το ύψος του γεωμετρικού σχήματος.
Τύπος 2: R = S / (A * 2), όπου S είναι η περιοχή του διαμαντιού και Α είναι το μήκος της πλευράς του.
Φόρμουλα 3: R = √ ((S * sin A) / 4), όπου S - είναι η περιοχή του ρόμβου, και Α sin - ημιτονοειδές οξεία γωνία της γεωμετρικό σχήμα.
Τύπος 4: R = B * D / (√ (² + ²), όπου Β και Γ είναι τα μήκη των διαγωνίων του γεωμετρικού σχήματος.
Τύπος 5: R = B * sin (A / 2), όπου B είναι η διαγώνια του ρομβοειδούς και A είναι η γωνία στις κορυφές που συνδέουν τη διαγώνιο.
Η ακτίνα του κύκλου που είναι εγγεγραμμένη στο τρίγωνο
Εάν στην κατάσταση του προβλήματος σας δοθούν τα μήκη όλων των πλευρών του σχήματος, τότε πρώτα υπολογίστε την περίμετρο του τριγώνου (P), και στη συνέχεια το ημιπερατόμετρο (n):
P = A + B + B, όπου A, B, B είναι τα μήκη των πλευρών του γεωμετρικού σχήματος.
n = n / 2.
Τύπος 1: R = √ ((η-Α) * (η-Β) * (η-Β) / η).
Και αν, γνωρίζοντας όλες τις ίδιες τρεις πλευρές, σας δίνεται η περιοχή του σχήματος, τότε μπορείτε να υπολογίσετε την επιθυμητή ακτίνα ως εξής.
Τύπος 2: R = S * 2 (Α + Β + Β)
Φόρμουλα 3: R = S / f = S / (A + B + C) / 2), όπου - το η - είναι semiperimeter γεωμετρικό σχήμα.
Φόρμουλα 4: R = (n - k) * TG (A / 2), όπου το η - είναι semiperimeter τρίγωνο Α - μία από τις πλευρές του, και TG (A / 2) - εφαπτομένη ήμισυ αυτής της πλευράς της αντίθετης γωνίας.
Και ο παρακάτω τύπος θα σας βοηθήσει να βρείτε την ακτίνα του κύκλου που είναι εγγεγραμμένη σε ένα ισόπλευρο τρίγωνο.
Τύπος 5: R = A * √3 / 6.
Η ακτίνα του κύκλου, που είναι εγγεγραμμένη σε ένα ορθό τρίγωνο
Εάν ένα πρόβλημα δεδομένης της μήκος των ποδιών και την υποτείνουσα, τότε η ακτίνα του εγγεγραμμένου κύκλου, όπως αναγνωρίζεται.
Τύπος 1: R = (A + B-C) / 2, όπου A, B - τα πόδια, C - η υποτείνουσα.
Σε περίπτωση που σας δοθούν μόνο δύο σκέλη, ήρθε η ώρα να θυμηθείτε το Πυθαγόρειο θεώρημα έτσι ώστε η hypotenuse να μπορεί να βρει και να χρησιμοποιήσει τον παραπάνω τύπο.
C = √ (Α2 + Β2).
Η ακτίνα του κύκλου, που είναι εγγεγραμμένη στην πλατεία
Ο κύκλος, ο οποίος είναι εγγεγραμμένος σε ένα τετράγωνο, χωρίζει όλες τις 4 πλευρές του ακριβώς στα μισά στα σημεία επαφής.
Τύπος 1: R = A / 2, όπου A - το μήκος της πλευράς του τετραγώνου.
Τύπος 2: R = S / (P / 2), όπου S και P είναι η περιοχή και η περίμετρος του τετραγώνου, αντίστοιχα.