Η γραμμή συντεταγμένων. Σημεία σχετικά με τη γραμμή συντεταγμένων. Πώς να κατασκευάσετε μια γραμμή συντεταγμένων

Για να πείτε ότι γνωρίζετε τα μαθηματικά είναι αδύνατο,εάν δεν ξέρετε πώς να χτίσετε γραφικά, να εκπροσωπήσετε ανισότητες στη γραμμή συντεταγμένων, να εργαστείτε με άξονες συντεταγμένων. Η οπτική συνιστώσα της επιστήμης είναι ζωτικής σημασίας, διότι χωρίς προφανή παραδείγματα σε τύπους και υπολογισμούς, μπορεί μερικές φορές να γίνει πολύ συγκεχυμένη. Σε αυτό το άρθρο, θα εξετάσουμε πώς να εργαστούμε με τους άξονες συντεταγμένων και να μάθουμε πώς να χτίζουμε γραφικά απλών λειτουργιών.

Εφαρμογή

Η γραμμή συντεταγμένων είναι η βάση του απλούστερου είδουςγραφήματα, τα οποία αντιμετωπίζει ο φοιτητής στην εκπαιδευτική πορεία του. Χρησιμοποιείται σε όλα σχεδόν τα μαθηματικά θέματα: στον υπολογισμό της ταχύτητας και του χρόνου, στην προβολή του μεγέθους των αντικειμένων και στον υπολογισμό της περιοχής τους, στην τριγωνομετρία όταν δουλεύουμε με sines και cosines.

Η κύρια τιμή μιας τέτοιας γραμμής είναι η ορατότητα. Δεδομένου ότι τα μαθηματικά είναι μια επιστήμη στην οποία απαιτείται υψηλό επίπεδο αφηρημένης σκέψης, τα γραφήματα βοηθούν στην αναπαράσταση ενός αντικειμένου στον πραγματικό κόσμο. Πώς συμπεριφέρεται; Σε ποιο σημείο του χώρου θα είναι μέσα σε λίγα δευτερόλεπτα, λεπτά, ώρες; Τι μπορείτε να πείτε σε σχέση με άλλα αντικείμενα; Ποια ταχύτητα έχει σε τυχαία επιλεγμένη χρονική στιγμή; Πώς να χαρακτηρίσετε το κίνημά του;

Και για την ταχύτητα δεν είναι χωρίς λόγο - είναι τηςσυχνά εμφανίζουν γραφήματα λειτουργιών. Και μπορούν επίσης να εμφανίσουν μια μεταβολή της θερμοκρασίας ή της πίεσης μέσα στο αντικείμενο, τις διαστάσεις του, τον προσανατολισμό του προς τον ορίζοντα. Έτσι, συχνά απαιτείται η κατασκευή μιας γραμμής συντεταγμένων στη φυσική.

Ένα μονοδιάστατο γράφημα

Υπάρχει η έννοια της πολυδιάστατοτητας. Σε μονοδιάστατο χώρο, μόνο ένας αριθμός είναι αρκετός για να καθορίσει τη θέση του σημείου. Αυτό συμβαίνει μόνο με τη χρήση της γραμμής συντεταγμένων. Εάν ο χώρος είναι διδιάστατος, απαιτούνται δύο αριθμοί. Τα διαγράμματα αυτού του τύπου χρησιμοποιούνται πολύ πιο συχνά, και λίγο περισσότερο στο άρθρο θα τα εξετάσουμε αναγκαστικά.

Τι μπορείτε να δείτε με σημεία στον άξονα, εάναυτή είναι μόνο μία; Μπορείτε να δείτε το μέγεθος του αντικειμένου, τη θέση του στο διάστημα σε σχέση με κάποιο "μηδέν", δηλ. Το σημείο που επιλέχθηκε ως σημείο αναφοράς.

Η αλλαγή των παραμέτρων με την πάροδο του χρόνου δεν μπορεί να δει, αφού όλες οι ενδείξεις θα εμφανιστούν για μια συγκεκριμένη στιγμή. Αλλά με κάτι που πρέπει να ξεκινήσετε! Ας αρχίσουμε λοιπόν.

Πώς να χτίσετε έναν άξονα συντεταγμένων

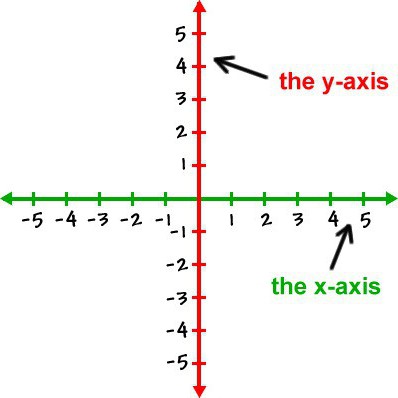
Αρχικά, πρέπει να εκτελέσετε μια οριζόντιαγραμμή - αυτός θα είναι ο άξονάς μας. Στη δεξιά πλευρά, "ακονίστε" το για να φανεί σαν ένα βέλος. Έτσι, υποδεικνύουμε την κατεύθυνση στην οποία θα αυξηθούν οι αριθμοί. Στην κατεύθυνση της μείωσης, το βέλος συνήθως δεν έχει ρυθμιστεί. Παραδοσιακά, ο άξονας δείχνει προς τα δεξιά, οπότε ακολουθούμε απλώς αυτόν τον κανόνα.

Βάλτε ένα μηδενικό σημάδι, το οποίο θα είναιεμφανίζει την προέλευση των συντεταγμένων. Αυτός είναι ο τόπος από τον οποίο μετράτε, είτε πρόκειται για μέγεθος, βάρος, ταχύτητα ή οτιδήποτε άλλο. Εκτός από το μηδέν, πρέπει πάντα να ορίσουμε την αποκαλούμενη τιμή διαίρεσης, δηλαδή να εισαγάγουμε το πρότυπο της μονάδας, σύμφωνα με το οποίο θα αναβάλλουμε ορισμένες ποσότητες στον άξονα. Αυτό πρέπει να γίνει για να μπορέσει να βρει το μήκος ενός τμήματος στη γραμμή συντεταγμένων.

Μέσα σε μια ισότιμη απόσταση από την άλλη θέσαμεσημεία ή "εγκοπές" στη γραμμή, και κάτω από αυτά θα γράψουμε 1,2,3 και ούτω καθεξής, αντίστοιχα. Και τώρα, όλα είναι έτοιμα. Αλλά με το προκύπτον χρονοδιάγραμμα, θα πρέπει να μάθετε πώς να εργαστείτε.

Τύποι σημείων στη γραμμή συντεταγμένων

Με μια ματιά στα προτεινόμενα στα εγχειρίδιατα στοιχεία γίνονται σαφή: τα σημεία στον άξονα μπορούν να βαφτούν ή να μην βαφτούν. Νομίζετε ότι αυτό είναι ατύχημα; Καθόλου! Ένα "στερεό" σημείο χρησιμοποιείται για μια μη αυστηρή ανισότητα - έναν τόμο που διαβάζεται ως "μεγαλύτερο ή ίσο με". Εάν είναι απαραίτητο να περιορίσουμε αυστηρά το διάστημα (για παράδειγμα, το "x" μπορεί να πάρει τιμές από μηδέν σε ένα, αλλά δεν το περιλαμβάνει), χρησιμοποιούμε ένα "κοίλο" σημείο, δηλαδή έναν μικρό κύκλο στον άξονα. Πρέπει να σημειωθεί ότι οι μαθητές δεν τους αρέσουν οι αυστηρές ανισότητες, επειδή είναι πιο δύσκολο να εργαστούν.

Ανάλογα με το σημείο που χρησιμοποιείτεστο γράφημα, θα καλούνται και τα κατασκευασμένα διαστήματα. Εάν η ανισότητα είναι μη αυστηρή και από τις δύο πλευρές, τότε αποκτάμε ένα τμήμα. Εάν, αφενός, είναι "ανοιχτό", τότε θα καλείται μισό διάστημα. Τέλος, εάν ένα τμήμα μίας ευθείας γραμμής οριοθετείται από δύο πλευρές με κοίλα σημεία, θα ονομάζεται ένα διάστημα.

Αεροπλάνο

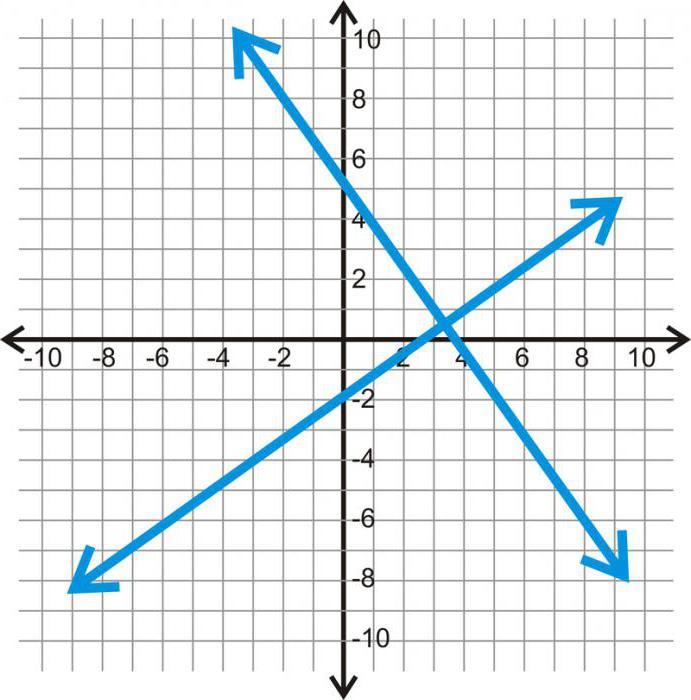
Κατά την κατασκευή δύο γραμμών στη συντεταγμένηεπίπεδο, μπορούμε ήδη να εξετάσουμε τα γραφήματα των λειτουργιών. Για παράδειγμα, η οριζόντια γραμμή θα είναι ο χρονικός άξονας και η κάθετη γραμμή θα είναι η απόσταση. Και τώρα είμαστε σε θέση να καθορίσουμε ποια απόσταση θα ξεπεράσει το αντικείμενο μέσα σε ένα λεπτό ή μια ώρα του δρόμου. Έτσι, η εργασία με ένα αεροπλάνο καθιστά δυνατή την παρακολούθηση της κατάστασης του αντικειμένου. Αυτό είναι πολύ πιο ενδιαφέρον από τη διερεύνηση μιας στατικής κατάστασης.

Το απλούστερο γράφημα σε ένα τέτοιο επίπεδο είναι μια ευθεία γραμμή, αντικατοπτρίζει τη συνάρτηση Y (X) = aX + b. Είναι η γραμμή κάμψη; Αυτό σημαίνει ότι το αντικείμενο αλλάζει τα χαρακτηριστικά του στη διαδικασία της έρευνας.

Φανταστείτε ότι στέκεστε στην οροφή ενός κτιρίου και κρατάτεστο απλωμένο χέρι μια πέτρα. Όταν την απελευθερώσετε, θα πετάξει κάτω, αρχίζοντας από μηδενική ταχύτητα. Αλλά σε ένα δευτερόλεπτο θα ξεπεράσει τα 36 χιλιόμετρα την ώρα. Η πέτρα θα συνεχίσει να επιταχύνει περαιτέρω και να τραβήξει την κίνηση της στο γράφημα, θα χρειαστεί να μετρήσετε την ταχύτητά της σε διάφορα σημεία του χρόνου, τοποθετώντας τα σημεία στον άξονα στις κατάλληλες θέσεις.

Τα σημάδια στην οριζόντια γραμμή συντεταγμένων στοτο προεπιλεγμένο όνομα είναι X1, X2, X3, και στην κατακόρυφη - Y1, Y2, Y3, αντίστοιχα. Με την προβολή τους σε ένα αεροπλάνο και την εύρεση διασταυρώσεων, βρίσκουμε θραύσματα του προκύπτοντος σχεδίου. Συνδυάζοντάς τα με μια γραμμή, έχουμε ένα γράφημα της λειτουργίας. Στην περίπτωση πέτρας που πέφτει, η τετραγωνική συνάρτηση θα έχει τη μορφή: Y (X) = aX * X + bX + c.

Μεγέθυνση

Φυσικά, δεν είναι απαραίτητο να εκθέσετε δίπλαδιαιρέσεις με άμεσες ακέραιες τιμές. Εάν εξετάζετε την κίνηση ενός σαλιγκαριού, το οποίο σέρνει με ταχύτητα 0,03 μέτρα ανά λεπτό, ρυθμίστε τις τιμές στην ευθεία της συντεταγμένης ως κλάσματα. Σε αυτή την περίπτωση, ορίστε την τιμή διαίρεσης ως 0,01 μέτρα.

Είναι ιδιαίτερα βολικό να πραγματοποιείτε τέτοια σχέδια σε ένα σημειωματάριοστο κλουβί - εδώ μπορείτε να δείτε αμέσως αν υπάρχει αρκετό χώρο στο φύλλο για το πρόγραμμά σας, δεν θα αφήσετε τα πεδία. Η αντοχή του στον υπολογισμό είναι απλή, επειδή το πλάτος του κυττάρου σε ένα τέτοιο φορητό υπολογιστή είναι 0,5 εκατοστά. Ήταν απαραίτητο - μείωσε το σχήμα. Από την αλλαγή στην κλίμακα του γραφήματος, δεν θα χάσει και δεν θα αλλάξει τις ιδιότητές του.

Συντεταγμένες ενός σημείου και ενός τμήματος

Όταν το μάθημα δίνει ένα μαθηματικό πρόβλημα, στοΜπορεί να περιέχει παραμέτρους διαφόρων γεωμετρικών μορφών, τόσο υπό τη μορφή μήκους πλευρών, περιμέτρου, περιοχής, και υπό μορφή συντεταγμένων. Σε αυτή την περίπτωση, μπορεί να χρειαστεί να χτίσετε ένα σχήμα και να πάρετε κάποια δεδομένα σχετικά με αυτό. Ανακύπτει το ερώτημα: πώς να βρείτε τις απαιτούμενες πληροφορίες σχετικά με τη γραμμή συντεταγμένων; Και πώς να οικοδομήσουμε μια φιγούρα;

Για παράδειγμα, μιλάμε για ένα σημείο. Στη συνέχεια, το κεφαλαίο γράμμα θα εμφανιστεί στην κατάσταση του προβλήματος και στις παρενθέσεις θα υπάρχουν πολλά ψηφία, συνήθως δύο (που σημαίνει ότι θα μετρήσουμε σε δισδιάστατο χώρο). Εάν υπάρχουν τρεις αριθμοί στις παρενθέσεις που έχουν γραφτεί μέσα από ένα ερωτηματικό ή ένα κόμμα, είναι ένας τρισδιάστατος χώρος. Κάθε μία από τις τιμές είναι η συντεταγμένη στον αντίστοιχο άξονα: πρώτα κατά μήκος της οριζόντιας (X), στη συνέχεια κατά την κάθετη (Y).

Θυμηθείτε πώς να χτίσετε ένα κομμάτι; Πήγατε μέσα από αυτή τη γεωμετρία. Εάν υπάρχουν δύο σημεία, τότε μπορείτε να σχεδιάσετε μια ευθεία γραμμή μεταξύ τους. Οι συντεταγμένες τους υποδεικνύονται σε παρενθέσεις, εάν εμφανιστεί ένα τμήμα στο πρόβλημα. Για παράδειγμα: Α (15, 13) - Β (1, 4). Για να δημιουργήσετε μια τέτοια γραμμή, πρέπει να εντοπίσετε και να επισημάνετε σημεία στο επίπεδο συντεταγμένων και, στη συνέχεια, να τα συνδέσετε. Αυτό είναι όλο!

Και οποιαδήποτε πολύγωνα, όπως γνωρίζετε, μπορούν να σχεδιαστούν με τη βοήθεια τμημάτων γραμμών. Το πρόβλημα επιλύεται.

Υπολογισμοί

Ας υποθέσουμε ότι υπάρχει ένα αντικείμενο, μια θέσηπου χαρακτηρίζεται από δύο αριθμούς κατά μήκος του άξονα Χ: αρχίζει από το σημείο με τη συντεταγμένη (-3) και τελειώνει στο (+2). Αν θέλουμε να γνωρίζουμε το μήκος αυτού του αντικειμένου, τότε πρέπει να αφαιρέσουμε από τον μικρότερο αριθμό. Σημειώστε ότι ένας αρνητικός αριθμός απορροφά το σύμβολο αφαίρεσης, επειδή το "μείον ένα αρνητικό δίνει ένα πλεονέκτημα". Έτσι, προσθέτουμε (2 + 3) και παίρνουμε 5. Αυτό είναι το απαιτούμενο αποτέλεσμα.

Ένα άλλο παράδειγμα: μας δίνεται το τελικό σημείο και το μήκος του αντικειμένου, αλλά δεν δίνεται η αρχική (και πρέπει να το βρείτε). Ας η θέση του ένα ορισμένο σημείο θα είναι (6), και το μέγεθος του αντικειμένου που μελετάται - (4). Αφαιρώντας τη διάρκεια των τελικών συντεταγμένων, παίρνουμε την απάντηση. Σύνολο: (6 - 4) = 2.

Αρνητικοί αριθμοί

Συχνά απαιτείται να εργαστείτεαρνητικές τιμές. Σε αυτή την περίπτωση, θα ακολουθήσουμε τον άξονα συντεταγμένων προς τα αριστερά. Για παράδειγμα, ένα αντικείμενο ύψους 3 cm επιπλέει στο νερό. Τρίτον, βυθίζεται σε υγρό, τα δύο τρίτα είναι στον αέρα. Στη συνέχεια, επιλέγοντας την επιφάνεια του νερού ως άξονα, χρησιμοποιούμε δύο στοιχειώδεις αριθμούς για να υπολογίσουμε την επιφάνεια του αντικειμένου: η κορυφή του αντικειμένου έχει συντεταγμένη (+2) και το κάτω (-1) εκατοστό.

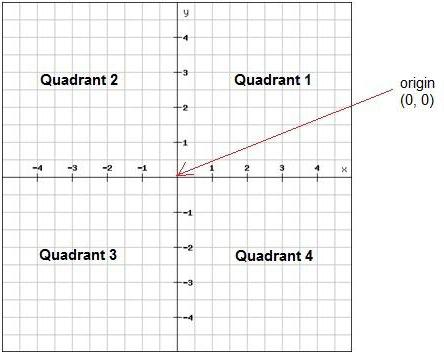
Δεν είναι δύσκολο να δούμε ότι στην περίπτωση του yΜας σχηματίζονται τέσσερα τέταρτα της γραμμής συντεταγμένων. Κάθε ένα από αυτά έχει τον δικό του αριθμό. Στο πρώτο (πάνω δεξιά) μέρος θα υπάρχουν σημεία με δύο θετικές συντεταγμένες, στη δεύτερη - στα αριστερά από την κορυφή - οι τιμές κατά μήκος του άξονα "x" θα είναι αρνητικές και σύμφωνα με το "igrik" - θετικές. Ο τρίτος και ο τέταρτος μετριούνται περαιτέρω προς τα αριστερά.

Σημαντική ιδιοκτησία

Γνωρίζετε ότι μια ευθεία γραμμή μπορεί να φανταστεί ωςάπειρο σύνολο σημείων. Μπορούμε να δούμε οποιουσδήποτε αριθμούς αξιών όσο θέλουμε σε κάθε πλευρά του άξονα, αλλά δεν θα συναντήσουμε επαναλαμβανόμενες. Αυτό φαίνεται αφελές και κατανοητό, αλλά αυτή η δήλωση προέρχεται από ένα σημαντικό γεγονός: σε κάθε αριθμό αντιστοιχεί ένα και μόνο ένα σημείο στη γραμμή συντεταγμένων.

Συμπέρασμα

Θυμηθείτε ότι οι άξονες, τα σχήματα και, αν είναι δυνατόν,τα γραφικά πρέπει να είναι κατασκευασμένα σύμφωνα με τον χάρακα. Μονάδες μετρήσεων εφευρέθηκαν από ένα άτομο όχι τυχαία - κάνοντας ένα λάθος στη σύνταξη, κινδυνεύετε να δείτε δεν είναι η εικόνα που θα έπρεπε να έχει αποδειχθεί.

Να είστε προσεκτικοί και προσεκτικοί στην οικοδόμησηγραφήματα και υπολογισμούς. Όπως και κάθε επιστήμη που μελετά στο σχολείο, τα μαθηματικά αγαπούν την ακρίβεια. Προσθέστε μια μικρή προσπάθεια, και οι καλές βαθμολογίες δεν θα πάρουν πολύ.