Ο αλγόριθμος Kruskal - η κατασκευή του βέλτιστου σκελετού

Στις αρχές του 19ου αιώνα, το γεωμετρικό από το Βερολίνο, Jacob Steinerορίστε το έργο του πώς να συνδέσετε τα τρία χωριά έτσι ώστε το μήκος τους να ήταν το συντομότερο. Στη συνέχεια, γενικεύτηκε αυτό το πρόβλημα: απαιτείται να βρεθεί ένα σημείο στο αεροπλάνο έτσι ώστε η απόσταση από αυτό σε n άλλα σημεία ήταν η μικρότερη. Τον 20ο αιώνα συνεχίστηκαν οι εργασίες για το θέμα αυτό. Αποφασίστηκε να ληφθούν πολλά σημεία και να συνδεθούν με τέτοιο τρόπο ώστε η απόσταση μεταξύ τους να ήταν η συντομότερη. Πρόκειται για μια ειδική περίπτωση του προβλήματος που εξετάζουμε.

Άπληστοι αλγόριθμοι

Ο αλγόριθμος Kruskal αναφέρεται σε "άπληστους" αλγόριθμους(ονομάζονται επίσης κλίση). Η ουσία αυτών - η μεγαλύτερη νίκη σε κάθε βήμα. Δεν είναι πάντοτε αλγόριθμοι "άπληστοι" που δίνουν την καλύτερη λύση στο έργο. Υπάρχει μια θεωρία που δείχνει ότι όταν εφαρμόζονται σε συγκεκριμένα προβλήματα, παρέχουν τη βέλτιστη λύση. Αυτή είναι η θεωρία των matroids. Ο αλγόριθμος Kruskal σχετίζεται με τέτοια προβλήματα.

Βρίσκοντας τον σκελετό του ελάχιστου βάρους

Ο υπό εξέταση αλγόριθμος κατασκευάζει ένα βέλτιστοτον σκελετό του γραφήματος. Το πρόβλημα είναι το εξής. Dan μη-κατευθυνόμενο γράφημα χωρίς παράλληλες ακμές και βρόχους, και το σύνολο των ακμών δίνεται η συνάρτηση βάρους W, η οποία εκχωρεί τον αριθμό σε κάθε ακμή e - βάρος νεύρωση - w (e). Το βάρος κάθε υποσυνόλου του συνόλου των άκρων καθορίζεται από το άθροισμα των βαρών των άκρων του. Απαιτείται να βρεθεί ο σκελετός του μικρότερου βάρους.

Περιγραφή

Ο αλγόριθμος Kruskal λειτουργεί έτσι. Πρώτον, όλες οι άκρες του αρχικού γραφήματος είναι διατεταγμένες κατά σειρά αυξανόμενων βαρών. Αρχικά, το πλαίσιο δεν περιέχει άκρα, αλλά περιλαμβάνει όλες τις κορυφές του γραφήματος. Μετά το επόμενο βήμα του αλγορίθμου, προστίθεται ένα άκρο στο ήδη κατασκευασμένο τμήμα του πλαισίου, το οποίο είναι ένα δάσος εκτάσεως. Δεν επιλέγεται αυθαίρετα. Όλες οι άκρες του γραφήματος που δεν ανήκουν στον σκελετό μπορούν να ονομάζονται κόκκινο και πράσινο. Οι κορυφές κάθε κόκκινου πλευρού βρίσκονται σε μία συνιστώσα της συνδεσιμότητας του δάσους που κατασκευάζεται και οι κορυφές του πράσινου βρίσκονται σε διαφορετικές συνιστώσες. Επομένως, αν προσθέσετε ένα κόκκινο άκρο εκεί, εμφανίζεται ένας κύκλος και, αν το πράσινο - στο προκύπτον βήμα για το δάσος, η συνιστώσα συνδεσιμότητας θα είναι μικρότερη κατά μία. Έτσι, δεν μπορεί να προστεθεί κόκκινη άκρη στην προκύπτουσα κατασκευή, αλλά μπορεί να προστεθεί κάθε πράσινο άκρο για να πάρει το δάσος. Και προστίθεται μια πράσινη πλευρά με ελάχιστο βάρος. Ως αποτέλεσμα, αποκτάται ο σκελετός του μικρότερου βάρους.

Εφαρμογή

Αναφέρετε το τρέχον δάσος F. Αυτός χωρίζει το σύνολο των κορυφών στον τομέα της συνδεσιμότητας (έντυπα ένωσή τους F, και είναι ξένα μεταξύ τους). Τα κόκκινα άκρα έχουν και τις δύο κορυφές σε ένα μέρος. Μέρος (x) - η λειτουργία που για κάθε κορυφή x επιστρέφει ένα τμήμα του ονόματος, ανήκει x. Unite (x, y) - μια διαδικασία που χτίζει ένα νέο διαμέρισμα, που αποτελείται από το συνδυασμό των τμημάτων Χ και Υ και όλα τα άλλα μέρη. Έστω n ο αριθμός των ακμών του γραφήματος. Όλες αυτές οι έννοιες που περιλαμβάνονται στον αλγόριθμο του Kruskal. Εφαρμογή:

1. Τοποθετήστε όλες τις άκρες του γραφήματος από το 1ο έως το nth ascending weights. (ai, bi είναι οι κορυφές της άκρης με το δείκτη i).

2. για i = 1 έως n.

3. x: = Μέρος (ai).

4. y: = Μέρος (bi).

5. Εάν το x δεν είναι ίσο με το y τότε Unite (x, y), συμπεριλάβετε την άκρη με τον αριθμό i στο F.

Σωστότητα

Έστω T - πλαίσιο του αρχικού γραφήματος κατασκευάστηκε χρησιμοποιώντας τον αλγόριθμο Kruskal και S - αυθαίρετη πλαίσιό του. Πρέπει να αποδείξουμε ότι w (T) δεν είναι μεγαλύτερο από w (S).

Έστω M το σύνολο των άκρων του S, P το σύνολο των άκρωνT. Εάν S δεν είναι ίσο με Τ, τότε υπάρχει μια ακμή et σκελετού Τ, που δεν ανήκουν στο S. S. et εφάπτονται του κύκλου, αυτό ονομάζεται C. C αφαιρέσετε από οποιεσδήποτε es άκρη, που ανήκουν S. Έχουμε λάβει ένα νέο πλαίσιο, διότι ακμές και υπάρχουν τόσα κορυφές σε αυτό. Το βάρος του δεν είναι μεγαλύτερο από w (S), δεδομένου ότι w (et) δεν είναι πλέον w (ES) σε μια δύναμη αλγόριθμο Kruskal. Αυτή η λειτουργία (υποκατάστατο νευρώσεις Τ S στις νευρώσεις) θα επαναληφθεί για όσο διάστημα λαμβάνετε T. Το βάρος του κάθε μετέπειτα λαμβανόμενου πλαισίου δεν είναι μεγαλύτερη από την προηγούμενη βάρος, πράγμα που σημαίνει ότι w (T) δεν είναι μεγαλύτερο από w (S).

Επίσης, η ορθότητα του αλγορίθμου Kruskal προκύπτει από το θεώρημα Rado-Edmonds για τα matroids.

Παραδείγματα εφαρμογής του αλγορίθμου Kruskal

Λαμβάνοντας ένα γράφημα με κορυφές a, b, c, d, e και άκρες (a,β), (α, ε), (β, γ), (b, e), (c, d), (c, e), (d, e). Τα βάρη των άκρων φαίνονται στον πίνακα και στο σχήμα. Αρχικά, η κατασκευή του δάσους F περιέχει όλες τις κορυφές του γραφήματος και δεν περιέχει ούτε μία άκρη. Αλγόριθμος Kruskal προσθέστε πρώτη νεύρωση (α, ε), δεδομένου ότι το βάρος είχε το χαμηλότερο, και οι κορυφές Α και Ε είναι σε διαφορετικά συστατικά συνδεσιμότητα ξυλείας F (νεύρωση (α, ε) είναι πράσινη), τότε η νεύρωση (c, d), επειδή ότι τουλάχιστον το βάρος αυτό ακμή των ακμών γραφήματος, που δεν ανήκουν σε F, και είναι πράσινο, τότε για τους ίδιους λόγους προκύψουν ακμή (a, b). Αλλά η ακμή (β, ε) έχει περάσει, παρά το γεγονός ότι ο ίδιος και το ελάχιστο βάρος των υπολοίπων άκρων, επειδή είναι κόκκινο: οι κορυφές Β και Ε ανήκουν στην ίδια συνιστώσα της σύνδεσης των δασών F, δηλαδή, αν προσθέσουμε σε F την άκρη (β, ε), σχηματίζεται κύκλου. Στη συνέχεια, προστίθεται το πράσινο άκρο (b, c), το κόκκινο άκρο (c, e) παραλείπεται και στη συνέχεια d, e. Έτσι, οι ακμές (a, e), (c, d), (a, b), (b, c) προστίθενται ακολουθιακά. Από αυτό, συνίσταται ο βέλτιστος σκελετός του αρχικού γραφήματος. Αυτός είναι ο τρόπος με τον οποίο ο αλγόριθμος λειτουργεί σε αυτήν την περίπτωση Βαμμένα. Ένα παράδειγμα δείχνει αυτό.

Το σχήμα δείχνει ένα γράφημα που αποτελείται από δύο συνιστώσες συνδεσιμότητας. Οι έντονες γραμμές δείχνουν τις άκρες του βέλτιστου πλαισίου (πράσινο), που έχουν κατασκευαστεί χρησιμοποιώντας τον αλγόριθμο Kruskal.

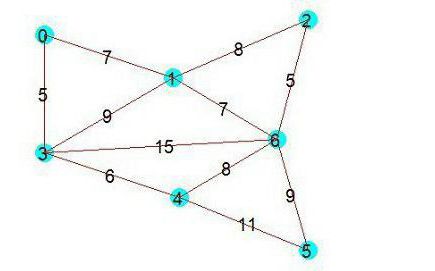
Το επάνω σχήμα δείχνει το αρχικό γράφημα, και στο χαμηλότερο - τον σκελετό του ελάχιστου βάρους, που κατασκευάστηκε για αυτό με τη βοήθεια του αλγορίθμου που εξετάστηκε.

Η ακολουθία των προστιθέμενων άκρων: (1.6); (0,3), (2,6) ή (2,6), (0,3) - δεν έχει σημασία. (3.4). (0,1), (1,6) ή (1,6), (0,1), είναι επίσης αδιάφορη (5,6).

Ο αλγόριθμος του Kruskal βρίσκει πρακτική εφαρμογή, για παράδειγμα, για τη βελτιστοποίηση των μαξιλαριών επικοινωνίας, των δρόμων σε νέες γειτονιές στις τοποθεσίες κάθε χώρας, αλλά και σε άλλες περιπτώσεις.