Το αόριστο ολοκλήρωμα. Υπολογισμός αόριστων ολοκληρωμάτων

Ένα από τα βασικά τμήματα του μαθηματικούη ανάλυση είναι ο ολοκληρωμένος υπολογισμός. Καλύπτει το ευρύτερο πεδίο αντικειμένων, όπου το πρώτο είναι αόριστο ενιαίο σύνολο. Για να το τοποθετήσουμε, είναι ένα κλειδί, που ακόμη και στο γυμνάσιο αποκαλύπτει έναν αυξανόμενο αριθμό προοπτικών και ευκαιριών που περιγράφουν τα ανώτερα μαθηματικά.

Εμφάνιση

Με την πρώτη ματιά, το ενιαίο φαίνεται απίστευτασύγχρονο, σχετικό, αλλά στην πράξη αποδεικνύεται ότι εμφανίστηκε το 1800 π.Χ. Η πατρίδα θεωρείται επισήμως ως Αίγυπτος, αφού δεν είχαμε νωρίτερα αποδεικτικά στοιχεία για την ύπαρξή της. Αυτός, εξαιτίας της έλλειψης πληροφόρησης, όλη αυτή τη στιγμή τοποθετείται ακριβώς ως φαινόμενο. Επιβεβαίωσε για μια ακόμη φορά το επίπεδο ανάπτυξης της επιστήμης μεταξύ των λαών εκείνων των χρόνων. Τέλος βρέθηκαν τα έργα αρχαίων Ελλήνων μαθηματικών του 4ου αιώνα π.Χ. Περιέγραψαν μια μέθοδο στην οποία εφαρμόστηκε ένα αόριστο ενιαίο σύνολο, το ουσιώδες στοιχείο του οποίου ήταν να βρούμε τον όγκο ή την περιοχή μιας καμπυλόγραμμης μορφής (τρισδιάστατα και δισδιάστατα επίπεδα, αντίστοιχα). Η αρχή του υπολογισμού βασίστηκε στη διαίρεση του αρχικού αριθμού σε απειροελάχιστα στοιχεία, υπό τον όρο ότι ο όγκος (περιοχή) τους είναι ήδη γνωστός. Με την πάροδο του χρόνου, η μέθοδος αυξήθηκε, ο Archimedes το χρησιμοποίησε για να βρει την περιοχή της παραβολής. Ανάλογοι υπολογισμοί ταυτόχρονα διεξήχθησαν από επιστήμονες στην αρχαία Κίνα, επιπλέον, ήταν εντελώς ανεξάρτητοι από τους Έλληνες αδελφούς στην επιστήμη.

Ανάπτυξη

Η επόμενη ανακάλυψη στον 11ο αιώνα είναι ήδη η εποχή της εποχής μαςτο έργο του Αραβικού λόγιος «βαγόνι» Abu Ali al-Basri, ο οποίος έσπρωξε τα όρια της ήδη γνωστά, προήλθαν από το ενιαίο τύπο για τον υπολογισμό των ποσών των ποσών και των βαθμών από τον πρώτο έως τον τέταρτο, χρησιμοποιώντας γι 'αυτό γνωρίζουμε τη μέθοδο της μαθηματικής επαγωγής.

Τα μυαλά της νεωτερικότητας θαυμάζουν τον αρχαίο τρόποΟι Αιγύπτιοι δημιούργησαν εκπληκτικά μνημεία αρχιτεκτονικής, χωρίς ειδικές συσκευές, εκτός ίσως από τα χέρια τους, αλλά δεν είναι η δύναμη των μυαλών των επιστημόνων εκείνης της εποχής όχι λιγότερο θαύμα; Σε σύγκριση με τους σημερινούς χρόνους, η ζωή τους φαίνεται σχεδόν πρωτόγονη, αλλά η λύση αόριστων ολοκληρωμάτων προέκυψε παντού και χρησιμοποιήθηκε στην πράξη για περαιτέρω ανάπτυξη.

Το επόμενο βήμα συνέβη στον XVI αιώνα, ότανο Ιταλός μαθηματικός Cavalieri συνήγαγε τη μέθοδο του αδιαίρετου, την οποία πήρε ο Pierre Fermat. Είναι αυτά τα δύο άτομα που έθεσαν τα θεμέλια για τον σύγχρονο ολοκληρωτικό λογισμό που είναι γνωστός αυτή τη στιγμή. Συνδύασαν τις έννοιες της διαφοροποίησης και της ολοκλήρωσης, οι οποίες προηγουμένως θεωρούνταν αυτόνομες μονάδες. Σε γενικές γραμμές, τα μαθηματικά εκείνης της εποχής ήταν κατακερματισμένα, το σωματίδιο των συμπερασμάτων υπήρχε από μόνο του, έχοντας ένα περιορισμένο πεδίο εφαρμογής. Το μονοπάτι της ενοποίησης και της αναζήτησης κοινών θεμάτων ήταν το μόνο σωστό εκείνο το χρονικό διάστημα, χάρη του οποίου η σύγχρονη μαθηματική ανάλυση ήταν σε θέση να αναπτυχθεί και να αναπτυχθεί.

Με την πάροδο του χρόνου, όλα άλλαξαν και ο χαρακτηρισμόςενσωματωμένο συμπεριλαμβανομένων. Σε γενικές γραμμές, ορίστηκε από επιστήμονες που ήταν σε αυτό το βαθμό, για παράδειγμα, ο Newton χρησιμοποίησε ένα τετράγωνο εικονίδιο στο οποίο έβαλε μια ενοποιήσιμη λειτουργία ή απλά το έβαλε μαζί.

Αυτή η διαμάχη κράτησε μέχρι τον XVII αιώνα,όταν ο Gottfried Leibnitz, ένα σημάδι για όλη τη θεωρία της μαθηματικής ανάλυσης, εισήγαγε το σύμβολο τόσο οικείο για μας. Ένα επίμηκες "S" βασίζεται πραγματικά σε αυτό το γράμμα του λατινικού αλφαβήτου, καθώς υποδηλώνει το άθροισμα των αντίθετων παραγόντων. Το όνομα του ολοκληρώματος οφείλεται στον Jacob Bernoulli μετά από 15 χρόνια.

Τυπικός ορισμός

Το αόριστο σύνολο εξαρτάται άμεσα από τον ορισμό ενός πρωτόγονου, επομένως θα το εξετάσουμε πρώτα.

Ο αντισυμβαλλόμενος είναι η αντίστροφη λειτουργία.παράγωγο, στην πράξη ονομάζεται επίσης πρωτόγονο. Διαφορετικά: το πρωτόγονο της συνάρτησης d είναι μια τέτοια συνάρτηση D, η παράγωγος της οποίας είναι ίση με v <=> V "= v. Η αναζήτηση πρωτόγονου είναι ο υπολογισμός ενός αόριστου ολοκλήρου και αυτή η ίδια η διαδικασία ονομάζεται ολοκλήρωση.

Παράδειγμα:

Λειτουργία s (y) = y³και το αντισεισμικό S (y) = (y⁴/ 4).

Το σύνολο όλων των αντισυμβαλλομένων της εν λόγω συνάρτησης είναι το αόριστο ολοκλήρωμα, το οποίο συμβολίζεται ως εξής: ∫v (x) dx.

Λόγω του γεγονότος ότι V (x) είναι μόνο μερικά(x) dx = V (x) + C, όπου το C είναι μια σταθερά. Με αυθαίρετη σταθερά εννοούμε οποιαδήποτε σταθερά, αφού το παράγωγο της είναι μηδέν.

Ιδιότητες

Οι ιδιότητες που κατέχει το αόριστο ολοκλήρωμα βασίζονται στον βασικό ορισμό και τις ιδιότητες των παραγώγων.

Εξετάστε τα βασικά σημεία:

• το ολοκλήρωμα του παραγώγου ενός πρωτόγονου είναι το ίδιο το πρωτόγονο συν μια αυθαίρετη σταθερά C <=> ∫V "(x) dx = V (x) + C.
• το παράγωγο του ολοκλήρου της συνάρτησης είναι η αρχική συνάρτηση <=> (∫v (x) dx) "= v (x);
• η σταθερά εξάγεται από το σύμβολο του ολοκλήρου <=> ∫kv (x) dx = kνv (x) dx, όπου το k είναι αυθαίρετο.
• το ολοκλήρωμα που λαμβάνεται από το άθροισμα είναι ταυτόσημα ίσο με το άθροισμα των ολοκληρώσεων <=> (v (y) + w (y)) dy = ∫v (y) dy + ∫w (y) dy.

Από τις δύο τελευταίες ιδιότητες, μπορούμε να συμπεράνουμε ότι το αόριστο ολοκλήρωμα είναι γραμμικό. Λόγω αυτού, έχουμε: ∫ (kv (y) dy + ∫ lw (y)) dy = k ∫v (y) dy + l∫w (y) dy.

Για να εδραιωθεί, εξετάστε παραδείγματα επίλυσης αόριστων ολοκληρωμάτων.

Είναι απαραίτητο να βρούμε το ολοκληρωμένο (3sinx + 4cosx) dx:

• ∫ (3sinx + 4cosx) dx = ∫3sinxdx + 4cosxdx = 3οsinxdx + 4∫cosxdx = 3 (-cosx) + 4sinx + C = 4sinx - 3cosx + C.

Από το παράδειγμα μπορούμε να συμπεράνουμε: δεν ξέρετε πώς να λύσετε αόριστα ολοκληρώματα; Απλά βρείτε όλα τα πρωτόγονα! Αλλά εξετάστε τις αρχές της αναζήτησης παρακάτω.

Μέθοδοι και παραδείγματα

Προκειμένου να επιλύσετε το ολοκλήρωμα, μπορείτε να καταφύγετε στις παρακάτω μεθόδους:

• χρησιμοποιήστε τον τελικό πίνακα.
• ενσωματώνονται σε μέρη?
• να ενσωματωθεί με την αντικατάσταση της μεταβλητής.
• αθροίζοντας το διακριτικό σήμα.

Πίνακες

Ο ευκολότερος και πιο ευχάριστος τρόπος. Προς το παρόν, η μαθηματική ανάλυση μπορεί να υπερηφανεύεται για αρκετά εκτεταμένους πίνακες, οι οποίοι περιέχουν τους βασικούς τύπους αόριστων ολοκληρώσεων. Με άλλα λόγια, υπάρχουν πρότυπα που έχουν προκύψει για εσάς και για σας, παραμένει μόνο να τα χρησιμοποιήσετε. Ακολουθεί μια λίστα με τις θέσεις των κύριων τραπεζιών στις οποίες μπορείτε να εμφανίσετε σχεδόν κάθε παράδειγμα που έχει μια λύση:

• ∫0dy = C, όπου C είναι σταθερά.
• ∫dy = y + C, όπου C είναι σταθερά.
• ∫yⁿdy = (y^{n + 1}) / (η + 1) + C, όπου το C είναι μια σταθερά και το η είναι ένας αριθμός διαφορετικός από έναν.
• ∫ (1 / y) dy = ln | y | + C, όπου C είναι σταθερά.
• ∫ε^ydy = e^y + C, όπου C είναι σταθερά.
• ∫k^ydy = (k^y/ ln k) + C, όπου το C είναι σταθερά.
• ∫cosydy = siny + C, όπου C είναι σταθερά.
• Inysinydy = -cosy + C, όπου C είναι σταθερά.
• ∫dy / cos²y = tgy + C, όπου C είναι σταθερά,
• Dydy / αμαρτία²y = -ctgy + C, όπου C είναι σταθερά.
• Dydy / (1 + y²) = arctgy + C, όπου C είναι σταθερά.
• ∫chydy = ντροπαλός + C, όπου C είναι σταθερά.
• ∫shydy = chy + C, όπου το C είναι μια σταθερά.

Εάν είναι απαραίτητο, κάντε μερικά βήματα, φέρτε το ενσωματωμένο στην τραπέζι και απολαύστε τη νίκη. Παράδειγμα: ∫cos (5x - 2) dx = 1 / 5cos (5x - 2) d (5x - 2) = 1/5 x sin (5x - 2) + C.

Με την απόφαση είναι σαφές ότι για το τραπέζι παράδειγμα το integrand δεν έχει συντελεστή 5. Προσθέτουμε, παράλληλα με αυτόν τον πολλαπλασιασμό κατά 1/5 έτσι ώστε η γενική έκφραση να μην αλλάζει.

Ενσωμάτωση σε μέρη

Εξετάστε δύο λειτουργίες - z (y) και x (y). Πρέπει να είναι συνεχώς διαφοροποιήσιμα σε ολόκληρο τον τομέα. Με μία από τις ιδιότητες της διαφοροποίησης, έχουμε: d (xz) = xdz + zdx. Η ενσωμάτωση και των δύο πλευρών της ισότητας, λαμβάνουμε: ∫d (xz) = (xdz + zdx) => zx = ∫zdx + ∫xdz.

Με την επανεγγραφή της λαμβανόμενης ισότητας, λαμβάνουμε έναν τύπο που περιγράφει τη μέθοδο ενσωμάτωσης σε μέρη: ∫zdx = zx - ∫xdz.

Γιατί χρειάζεται; Το γεγονός είναι ότι μερικά παραδείγματα μπορούν να απλουστευθούν, σχετικά μάλιστα, για να μειωθούν οι εestizdx στο ∫xdz, εάν το τελευταίο είναι κοντά σε πίνακα. Επίσης, αυτός ο τύπος μπορεί να εφαρμοστεί περισσότερες από μία φορές, επιτυγχάνοντας βέλτιστα αποτελέσματα.

Πώς να λύσουμε απεριόριστα ολοκληρώματα με αυτόν τον τρόπο:

• πρέπει να υπολογίσουμε το ∫ (s + 1) e^2sds

∫ (x + 1) e^2sds = {z = s + 1, dz = ds, y = 1 / 2e^2s, dy = ε^2χds} = ((s + 1) ε^2s) / 2-1 / 2οε^2sdx = ((s + 1) e^2s) / 2-e^2s/ 4 + C.

• πρέπει να υπολογίσετε τις εισροές

∫nsns = {z = lns, dz = ds / s, y = s, dy = ds} = slns - xs x ds / s = slns - Γ.

Μεταβλητή αντικατάσταση

Αυτή η αρχή της επίλυσης αόριστων ολοκληρωμάτων δεν είναιλιγότερη ζήτηση από τις προηγούμενες δύο, αν και πιο δύσκολη. Η μέθοδος είναι η εξής: ας V (x) είναι το ολοκλήρωμα κάποιας συνάρτησης v (x). Σε περίπτωση που το ίδιο το αναπόσπαστο μέρος του παραδείγματος συναντά μια ένωση, είναι πιθανό να μπερδευτεί και να πάρει τη λανθασμένη πορεία της απόφασης. Για να αποφευχθεί αυτό, γίνεται η μετάβαση από τη μεταβλητή x στο z, στην οποία η γενική έκφραση είναι οπτικά απλοποιημένη ενώ διατηρείται η εξάρτηση του z στο x.

Στη μαθηματική γλώσσα, φαίνεται σαν εξής: ∫v (x) dx = v (y (z)) y "(z) dz = V^-1(x)), όπου x = y (z) είναι μια μετάθεση. Και, φυσικά, η αντίστροφη συνάρτηση z = y^-1(x) περιγράφει πλήρως την εξάρτηση καιαλληλεξάρτηση μεταβλητών. Μια σημαντική σημείωση είναι ότι το διαφορικό dx αντικαθίσταται υποχρεωτικά από ένα νέο διαφορικό dz, αφού η αντικατάσταση μιας μεταβλητής σε ένα αόριστο ολοκλήρωμα συνεπάγεται την αντικατάστασή της με μια μεταβλητή παντού, και όχι μόνο στην ολοκλήραν.

Παράδειγμα:

• πρέπει να βρούμε ∫ (s + 1) / (s² + 2s - 5) ds

Εφαρμόστε την υποκατάσταση z = (s + 1) / (s²+ 2s-5). Στη συνέχεια dz = 2sds = 2 + 2 (s + 1) ds <=> (s + 1) ds = dz / 2. Ως αποτέλεσμα, έχουμε την ακόλουθη έκφραση, η οποία είναι πολύ εύκολο να υπολογιστεί:

∫ (s + 1) / (s²+ 2s-5) ds = (dz / 2) / z = 1 / 2in | z | + C = 1 / 2in | s²+ 2s-5 | + C;

• είναι απαραίτητο να βρούμε το ολοκλήρωμα 2^sε^sdx

Για να λύσετε, ξαναγράψτε την έκφραση με την ακόλουθη μορφή:

∫2^sε^sds = ∫ (2ε)^sds.

Σημειώστε με a = 2e (αυτό το βήμα δεν είναι υποκατάστατο του όρου, είναι ακόμα s), φέρουμε το φαινομενικά πολύπλοκο μας συστατικό στην στοιχειώδη πίνακα:

∫ (2ε)^sds = ∫a^sds = a^s / lna + C = (2e)^s / Ιη (2ε) + C = 2^sε^s / ln (2 + lne) + C = 2^sε^s / (ln2 + 1) + C.

Διακριτικό σήμα

Σε γενικές γραμμές, αυτή η μέθοδος αόριστων ολοκληρώσεων είναι ο δίδυμος αδερφός της αρχής της μεταβλητής αντικατάστασης, ωστόσο υπάρχουν διαφορές στη διαδικασία σχεδιασμού. Ας εξετάσουμε με περισσότερες λεπτομέρειες.

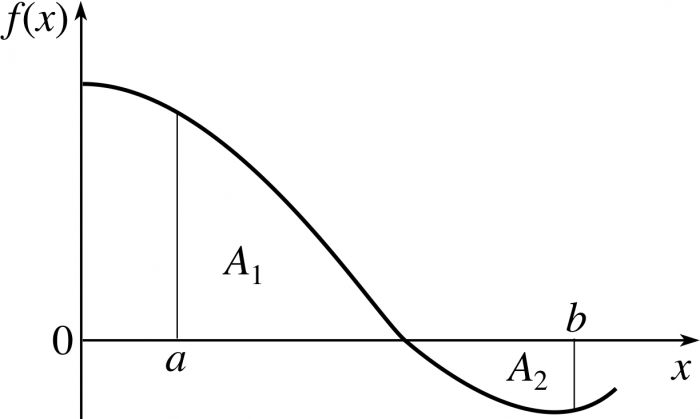
Αν το ∫v (x) dx = V (x) + C και y = z (x), τότε ∫v (y) dy = V (y) + C.

Επιπλέον, δεν μπορούμε να ξεχνάμε ασήμαντα ολοκληρωτικά μετασχηματισμούς, μεταξύ των οποίων:

• dx = d (x + a), όπου a είναι οποιαδήποτε σταθερά.
• dx = (1 / a) d (ax + b), όπου a είναι και πάλι μια σταθερά, αλλά δεν είναι ίση με το μηδέν.
• xdx = 1 / 2d (χ² + β).
• sinxdx = -d (cosx).
• cosxdx = d (sinx).

Αν εξετάσουμε τη γενική περίπτωση κατά τον υπολογισμό του απεριόριστου ολοκλήρου, τα παραδείγματα μπορούν να συνοψιστούν με τον γενικό τύπο w "(x) dx = dw (x).

Παραδείγματα:

• πρέπει να βρούμε ∫ (2s + 3)²ds, ds = 1/2d (2s + 3)

∫ (2s + 3)²ds = 1 / 2θ (2s + 3)²d (2s + 3) = (1/2) x ((2s + 3)²) / 3 + C = (1/6) χ (2s + 3)² + C;

∫tgsds = ∫sins / cossds = d (coss) / coss = -ln | coss | + C.

Ηλεκτρονική βοήθεια

Σε ορισμένες περιπτώσεις, η ευθύνη μπορεί να είναιή τεμπελιά, ή επείγουσα ανάγκη, μπορείτε να χρησιμοποιήσετε τις ηλεκτρονικές συμβουλές ή μάλλον να χρησιμοποιήσετε την αριθμομηχανή αόριστων ολοκληρωμάτων. Παρά την προφανή πολυπλοκότητα και διαμάχη των ολοκληρωμάτων, η λύση τους υπόκειται σε έναν συγκεκριμένο αλγόριθμο, ο οποίος βασίζεται στην αρχή "αν όχι ... τότε ...".

Φυσικά, ιδιαίτερα περίπλοκα παραδείγματα τέτοιωνη αριθμομηχανή δεν θα κυριαρχεί, καθώς υπάρχουν περιπτώσεις στις οποίες η λύση πρέπει να βρεθεί τεχνητά, "βίαια" με την εισαγωγή ορισμένων στοιχείων στη διαδικασία, επειδή τα αποτελέσματα δεν μπορούν να επιτευχθούν με προφανή μέσα. Παρά την αμφιλεγόμενη φύση αυτής της δήλωσης, είναι αλήθεια, δεδομένου ότι τα μαθηματικά, κατ 'αρχήν, είναι μια αφηρημένη επιστήμη και θεωρεί ότι η αναγκαιότητα επέκτασης των ορίων των δυνατοτήτων είναι το πρωταρχικό της καθήκον. Πράγματι, σύμφωνα με τις ομαλές διαδοχικές θεωρίες, είναι εξαιρετικά δύσκολο να κινηθείτε προς τα πάνω και να αναπτυχθούν, οπότε δεν πρέπει να υποθέσετε ότι τα παραδείγματα επίλυσης αόριστων ολοκληρωμάτων που δώσαμε είναι οι κορυφαίες δυνατότητες. Αλλά πίσω στην τεχνική πλευρά. Τουλάχιστον για να επαληθεύσετε τους υπολογισμούς, μπορείτε να χρησιμοποιήσετε τις υπηρεσίες στις οποίες τα όσα διατυπώθηκαν πριν από εμάς. Αν υπάρχει ανάγκη για αυτόματο υπολογισμό μιας περίπλοκης έκφρασης, τότε δεν θα κάνουν, θα πρέπει να καταφύγετε σε πιο σοβαρό λογισμικό. Αξίζει να δοθεί προσοχή κυρίως στο περιβάλλον MatLab.

Εφαρμογή

Επίλυση απεριόριστων ολοκληρωμάτων στην αρχήτο βλέμμα φαίνεται να απομακρύνεται τελείως από την πραγματικότητα, καθώς είναι δύσκολο να δούμε το προφανές επίπεδο εφαρμογής. Πράγματι, δεν μπορούν να χρησιμοποιηθούν απ 'ευθείας οπουδήποτε, αλλά θεωρούνται ότι αποτελούν απαραίτητο ενδιάμεσο στοιχείο στη διαδικασία λήψης λύσεων που χρησιμοποιούνται στην πράξη. Έτσι, η ολοκλήρωση είναι πίσω διαφοροποίηση, λόγω της οποίας συμμετέχει ενεργά στη διαδικασία επίλυσης των εξισώσεων.

Με τη σειρά τους, αυτές οι εξισώσεις έχουνάμεση επιρροή στη λύση των μηχανικών προβλημάτων, υπολογισμός των τροχιών και θερμική αγωγιμότητα - εν συντομία, ό, τι αποτελεί το παρόν και αποτελεί το μέλλον. Το αόριστο ολοκλήρωμα, τα παραδείγματα των οποίων θεωρήσαμε παραπάνω, είναι απλώς απλή σε πρώτη ματιά, δεδομένου ότι αποτελεί τη βάση για την πραγματοποίηση νέων και νέων ανακαλύψεων.